Como prever o valor de venda de uma casa?
October 22, 2018
Olá, seja bem vindo(a) a mais um tópico na série de estudo sobre Tensorflow. Hoje iremos implementar uma rede neural para uma tarefa de regressão em preços de imóveis. Problemas de regrssão são um importante assunto dentro da área de aprendizado de máquina. Espero que você já tenha preparado seu ambiente para rodar os scripts, senão, confira os links ao final do post e siga a opção desejada. Antes de continuar, você precisa estar familiarizado com os conceitos de aprendizado de máquina. Uma boa referência é o machine learning crash course produzido pela google.
Em um problema de regressão, pretendemos prever a saída que contém um valor contínuo, representando um preço ou uma probabilidade. Isso é diferente de um problema de classificação, em que pretendemos prever um rótulo discreto (por exemplo, quando uma imagem contém um cachorro ou um gato).

Este post tem o objetivo de construir um modelo para prever o preço médio das casas em um subúrbio de Boston em meados da década de 1970. Para fazer isso, forneceremos ao modelo alguns pontos de dados sobre o subúrbio, como a taxa de criminalidade e a taxa de imposto sobre a propriedade local. Ao terminar a leitura, você será capaz de:
- carregar o conjunto de dados Boston housing prices
- explorar e preprocessar os dados de treinamento
- construir seu modelo com o TensorFlow
- treinar, avaliar e fazer predições com seu modelo.
- Visualizar o histórico de erros e desempenho
Assim como no post anterior, vamos usar o pacote tf.keras, uma api de alto nível do TensorFlow para construir e treinar o modelo.
O trecho do código a seguir importa os pacotes necessários para nosso script rodar tranquilamente.
import tensorflow as tf
from tensorflow import keras
import numpy as np
Carregando o conjunto de dados de Imovéis em Boston
Este conjunto de dados é acessível diretamente no TensorFlow. Faça o download e embaralhe o conjunto de treinamento:
boston_housing = keras.datasets.boston_housing
(train_data, train_labels), (test_data, test_labels) = boston_housing.load_data()
# Shuffle the training set
order = np.argsort(np.random.random(train_labels.shape))
train_data = train_data[order]
train_labels = train_labels[order]
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/boston_housing.npz
57344/57026 [==============================] - 0s 0us/step
Este conjunto de dados é muito menor do que os outros com os quais já trabalhamos até agora: ele tem 506 exemplos no total são divididos entre exemplos de treinamento 404 e 102 exemplos de teste:
print("Training set: {}".format(train_data.shape)) # 404 examples, 13 features
print("Testing set: {}".format(test_data.shape)) # 102 examples, 13 features
O conjunto de dados contém 13 atributos diferentes:
- Taxa de criminalidade per capita.
- A proporção de terrenos residenciais zoneada para lotes com mais de 25.000 pés quadrados.
- A proporção de acres comerciais não varejistas por cidade.
- Variável dummy de Charles River (= 1 se o setor limite rio; 0 caso contrário).
- Concentração de óxidos nítricos (partes por 10 milhões).
- O número médio de quartos por habitação.
- A proporção de unidades ocupadas pelo proprietário construídas antes de 1940.
- Distâncias ponderadas para cinco centros de emprego em Boston.
- Índice de acessibilidade às autoestradas radiais.
- Taxa de imposto sobre propriedades de valor integral por US $ 10.000.
- Relação aluno-professor por cidade.
- 1000 * (Bk - 0,63) ** 2 onde Bk é a proporção de negros por cidade.
- Percentagem de status inferior da população.
Cada um desses atributos é armazenado usando uma escala diferente. Alguns atributos são representados por uma proporção entre 0 e 1, outros são intervalos entre 1 e 12, alguns são intervalos entre 0 e 100 e assim por diante. Isto ocorre com freqêuncia com dados do mundo real, e entender como explorar e limpar esses dados é uma habilidade importante a ser desenvolvida.
** Como cientista de dados, pense em possíveis benefícios e danos que as previsões de um modelo podem causar. Um modelo como este poderia reforçar preconceitos e disparidades sociais. Sua aplicação trará um recurso relevante para o problema que você deseja resolver ou irá introduzir um viés? **
Use a biblioteca pandas para exibir as primeiras linhas do conjunto de dados em uma tabela bem formatada:
import pandas as pd
column_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT']
df = pd.DataFrame(train_data, columns=column_names)
df.head()
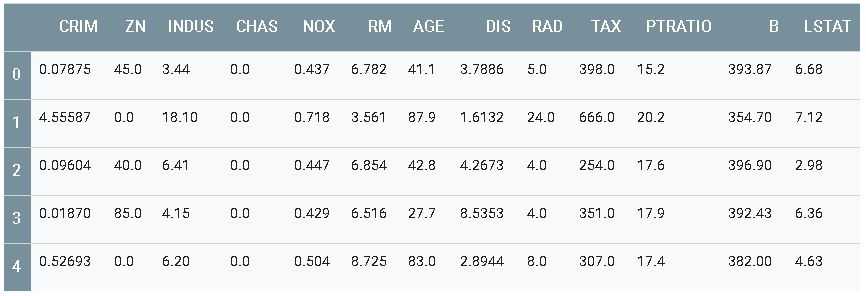
Os rótulos são os preços das casas em milhares de dólares. (Perceba que os preços são da metade dos anos 70).
print(train_labels[0:10]) # Display first 10 entries
[32. 27.5 32. 23.1 50. 20.6 22.6 36.2 21.8 19.5]
Pre-processamento
É recomendado normalizar atributos que usam escalas e intervalos diferentes. Para cada atributo, subtraia a média do recurso e divida pelo desvio padrão:
# Test data is *not* used when calculating the mean and std
mean = train_data.mean(axis=0)
std = train_data.std(axis=0)
train_data = (train_data - mean) / std
test_data = (test_data - mean) / std
print(train_data[0]) # First training sample, normalized
[-0.39725269 1.41205707 -1.12664623 -0.25683275 -1.027385 0.72635358
-1.00016413 0.02383449 -0.51114231 -0.04753316 -1.49067405 0.41584124
-0.83648691]
Embora o modelo possa convergir sem a normalização de recursos, isso dificulta o treinamento e torna o modelo resultante mais dependente da escolha de unidades usadas na entrada.
Construindo o modelo
Vamos construir nosso modelo. Aqui, usaremos um modelo sequencial com duas camadas ocultas densamente conectadas e uma camada de saída que retornará um único valor contínuo. As etapas de construção do modelo são agrupadas em uma função, build_model, pois criaremos um segundo modelo, mais adiante.
def build_model():
model = keras.Sequential([
keras.layers.Dense(64, activation=tf.nn.relu,
input_shape=(train_data.shape[1],)),
keras.layers.Dense(64, activation=tf.nn.relu),
keras.layers.Dense(1)
])
optimizer = tf.train.RMSPropOptimizer(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['mae'])
return model
model = build_model()
model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 64) 896
_________________________________________________________________
dense_1 (Dense) (None, 64) 4160
_________________________________________________________________
dense_2 (Dense) (None, 1) 65
=================================================================
Total params: 5,121
Trainable params: 5,121
Non-trainable params: 0
_________________________________________________________________
Treinando o modelo
O modelo é treinado para 500 épocas e registra a exatidão de treinamento e validação no objeto de histórico como visto no post anterior.
# Display training progress by printing a single dot for each completed epoch
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
if epoch % 100 == 0: print('')
print('.', end='')
EPOCHS = 500
# Store training stats
history = model.fit(train_data, train_labels, epochs=EPOCHS,
validation_split=0.2, verbose=0,
callbacks=[PrintDot()])
import matplotlib.pyplot as plt
def plot_history(history):
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Abs Error [1000$]')
plt.plot(history.epoch, np.array(history.history['mean_absolute_error']),
label='Train Loss')
plt.plot(history.epoch, np.array(history.history['val_mean_absolute_error']),
label = 'Val loss')
plt.legend()
plt.ylim([0, 5])
plot_history(history)
Visualize o progresso do treinamento do modelo usando as estatísticas armazenadas no objeto de histórico. A ideia é usar esses dados para determinar quanto tempo treinar antes que o modelo pare de progredir.
import matplotlib.pyplot as plt
def plot_history(history):
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Abs Error [1000$]')
plt.plot(history.epoch, np.array(history.history['mean_absolute_error']),
label='Train Loss')
plt.plot(history.epoch, np.array(history.history['val_mean_absolute_error']),
label = 'Val loss')
plt.legend()
plt.ylim([0, 5])
plot_history(history)
Este gráfico mostra pouca melhoria no modelo após cerca de 200 épocas. Vamos atualizar o método model.fit para parar automaticamente o treinamento quando a pontuação de validação não melhorar. Usaremos um retorno de chamada que testa uma condição de treinamento para cada época. Se uma determinada quantidade de épocas transcorrer sem mostrar melhoria, ele para automaticamente o treinamento.
model = build_model()
# The patience parameter is the amount of epochs to check for improvement
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=20)
history = model.fit(train_data, train_labels, epochs=EPOCHS,
validation_split=0.2, verbose=0,
callbacks=[early_stop, PrintDot()])
plot_history(history)
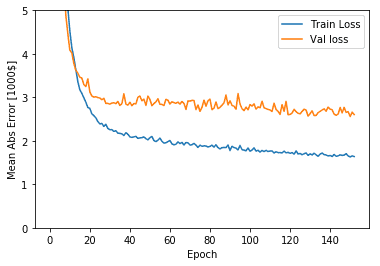
O gráfico mostra que o erro médio é de cerca de US $ 2.500. Isso não é bom, uma vez qeu US $ 2.500 não é uma quantia insignificante quando alguns dos rótulos custam apenas US $ 15.000.
Vamos ver como foi o desempenho do modelo no conjunto de testes:
[loss, mae] = model.evaluate(test_data, test_labels, verbose=0)
print("Testing set Mean Abs Error: ${:7.2f}".format(mae * 1000))
Testing set Mean Abs Error: $2713.16
Predição
Finalmente, obtenha alguns preços da habitação usando dados no conjunto de testes:
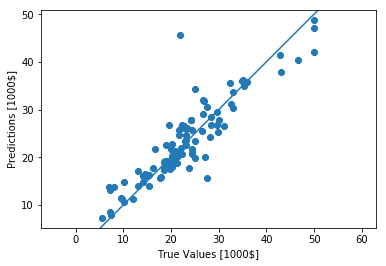
test_predictions = model.predict(test_data).flatten()
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [1000$]')
plt.ylabel('Predictions [1000$]')
plt.axis('equal')
plt.xlim(plt.xlim())
plt.ylim(plt.ylim())
_ = plt.plot([-100, 100], [-100, 100])
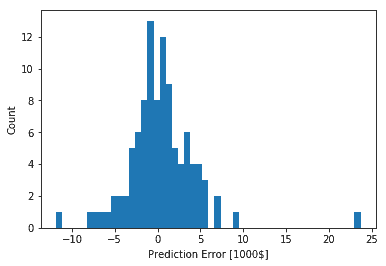
error = test_predictions - test_labels
plt.hist(error, bins = 50)
plt.xlabel("Prediction Error [1000$]")
_ = plt.ylabel("Count")
Resumo
Neste post você aprendeu algumas técnicas para lidar com um problema de regressão.
- Mean Squared Error (MSE) é uma função custo usada para problemas de regressão (diferente de problemas de classificação).
- Da mesma forma, as métricas de avaliação usadas para a regressão diferem da classificação. Uma métrica de regressão comum é o erro médio absoluto (MAE).
- Quando os atributos de dados de entrada possuem valores com intervalos diferentes, cada atributo deve ser dimensionado de forma independente.
- Se não houver muitos dados de treinamento, prefira uma pequena rede com poucas camadas ocultas para evitar o overfitting.
- A parada antecipada é uma técnica útil para evitar o overfitting.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.

